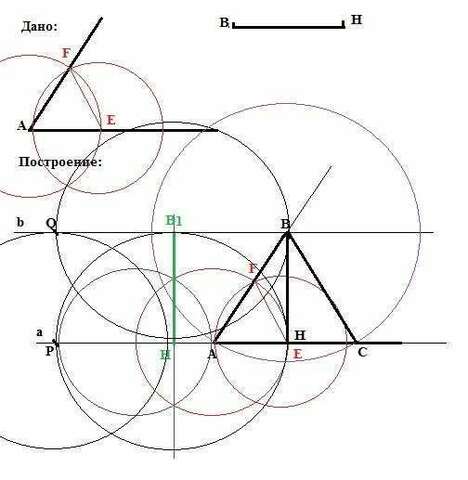
1. Сначала строим угол, равный данному. Для этого:
Проводим окружность с центром в вершине А ДАННОГО нам угла при основании произвольного (не очень большого) радиуса. Получаем "засечки" - точки Е и F на сторонах данного нам угла.
2. Пусть прямая "а" содержит одну из сторон данного нам угла.
На прямой "а" чертим окружность с центром в произвольной точке А радиусом АЕ.
Чертим окружность с центром в полученной точке Е (пересечение окружности с прямой "а") радиусом ЕF.
В точеке пересечения двух окружностей получаем точку F. Через точки А и F проводим прямую - получили вторую сторону угла, равного данному.
3. Проводим перпендикуляр к прямой "а". Для этого чертим окружность
произвольного радиуса с центром в произвольной точке на прямой (например, А). Проводим окружность с центром в одной из точек пересечения этой окружности с прямой тем же радиусом. Соединяем точки пересечения двух окружностей. Это - перпендикуляр к прямой "а".
4. Откладываем на перпендикуляре отрезок НВ1, равный данной нам высоте ВН в сторону от прямой, где расположена вторая сторона построенного угла и через конец полученного отрезка проводим прямую "b" , параллельно прямой "а".
Для этого:
a. Проводим окружность с центром в точке Н радиусом НВ.
b. На прямой "а" в месте пересечения с этой окружностью ставим
точку Р.
c. Проводим вторую окружность с центром в точке Р радиусом НВ.
d. Проводим третью окружность с центром в точке В1 радиусом НВ. Получаем точку Q на пересечении этой и предыдущей окружностей.
e. Через точки Q и B1 проводим прямую QВ1. Это и будет прямая "b", параллельная прямой "а".
5. На пересечении второй стороны построенного угла и прямой "b" ставим точку В.
6. Проводим окружность с центром в точке В радиусом ВА и в месте пересечения этой окружности ставим точку С.
Соединяем точки А,В и С. Искомый треугольник АВС построен.