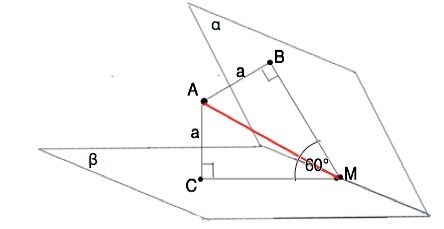
Пусть данная точка будет А, плоскости, между которыми она расположена – α и β.
Расстояние от точки до плоскости - длина отрезка, проведенного перпендикулярно к ней.
АВ ⊥ альфа, АС ⊥ бета. АВ=АС=а
Расстояние от точки до линии пересечения плоскостей - длина отрезка, проведенного перпендикулярно этой линии, т.е. ребру двугранного угла. АВ и АС лежат в плоскости, перпендикулярной двугранному углу, т.е. содержащей его линейный угол. АМ лежит в той же плоскости и потому перпендикулярна линии пересечения плоскостей.
ВМ и СМ - проекция наклонной АМ на данные плоскости, а т.к. расстояния от А до них равны, то ВМ=СМ.
Рассмотрим треугольники АВМ и АСМ. Оба прямоугольные с равными катетами и общей гипотенузой АМ. ⇒∆ АВМ=∆АСМ по трем сторонам.
∠АМВ=∠АМС=60°:2=30° ⇒
АМ=АВ:sin30°=а:1/2=2a Это ответ.