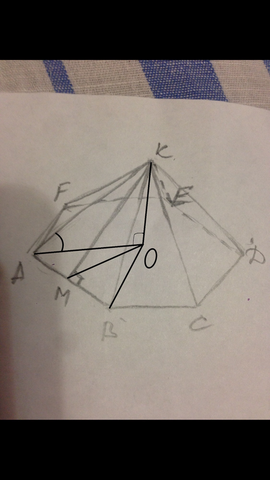
В треугольнике КАО катет КО лежит напротив угла в 30°, значит КО=КА/2=2√3/2=√3 дм.
АО²=КА²-КО²=12-3=9,
АО=3 дм.
Большие диагонали делят правильный шестиугольник на шесть правильных треугольников, значит ΔАОВ правильный.
В тр-ке АОВ высота ОМ=АО√3/2=3√3/2 дм (!).
Так как шестиугольник правильный и боковые рёбра пирамиды равны, то основание высоты - точка О, лежит в центре описанной и вписанной окружности, следовательно ОМ - радиус вписанной в основание окружности.
В прямоугольном тр-ке КМО КМ²=КО²+ОМ²=3+27/4=39/4,
Апофема КМ=√39/2 дм (!).