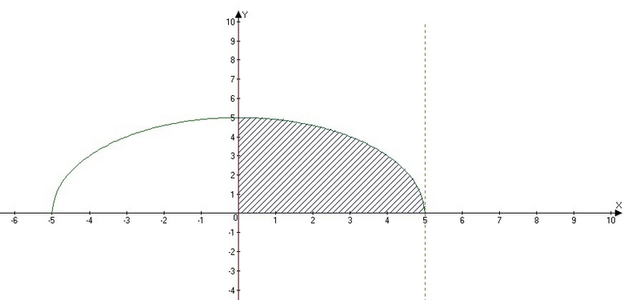
На графике мы видим выделенную область - сектор, площадь которой и нужно найти. Сначала найти общую площадь окружности с началом координат в точке (0;0) и центром 5.
S = pi *R^2 = 3,14*25 = 78,53
Теперь поделим S на 4, так как нам нужно узнать, сколько же составляет 1 четверть. S/4 = 19,63
Следовательно, ответ 19,63