Периметр 20-угольника равен 20 * 21, тогда точки делят периметр на отрезки длины 20 * 21/21 = 20 < 21. Значит, найдётся сторона 20-угольника, содержащая две точки 21-угольника.
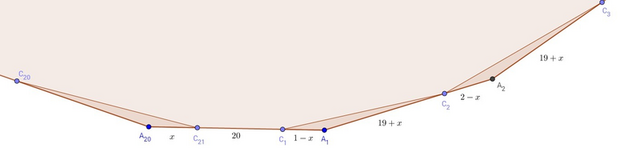
Пусть C1C2C3...C21 - 21-угольник, A1A2A3...A20 - 20-угольник, и точки C1 и C20 лежат на A20A1. Обозначим C1A1 = 1 - x, тогда A1C2 = 19 + x, C2A2 = 2 - x, A2C3 = 18 + x, ..., C20A20 = 20 - x, A20C21 = x. Очевидно, 0 ≤ x ≤ 1.
Разность площадей 20-угольника и 21-угольника равна сумме площадей треугольников C1A1C2, C2A2C3, C3A3C4, ..., C20A20C21. Так как все углы C1AC2, ..., C20A20C21 равны между собой и равны 180° - 360°/20 = 180° - 18°, то сумма площадей равна
S = 1/2 sin(180° - 18°) * ((1 - x)(19 + x) + (2 - x)(18 + x) + ... + (20 - x) x) = sin 18° ((1 - x)(19 + x) + (2 - x)(18 + x) + ... + (20 - x)x)/2
S(x) - квадратный трёхчлен относительно x, старший коэффициент отрицателен, поэтому максимум достигается в вершине квадратичной параболы. Так ка S(x) = S(1 - x), то парабола S(x) симметрична относительно x = 1/2, а значит, максимальное значение равно S(1/2).
Осталось вычислить значение. Выписываю сумму произведений в скобках:
0,5 * 19,5 + 1,5 * 18,5 + 2,5 * 17,5 + ... + 19,5 * 0,5 = (10 - 9,5)(10 + 9,5) + (10 - 8,5)(10 + 8,5) + ... + (10 - 0,5)(10 + 0,5) + (10 + 0,5)(10 - 0,5) + ... (10 + 9,5)(10 - 9,5) = 20 * 10² - 2 * 0.5² (1² + 3² + 5² + ... + 17² + 19²) = 2000 - 0.5 * 1330 = 1335
1² + 3² + ... + 19² можно посчитать вручную на листочке.
S(0.5) = 1335 sin18° / 2 - максимальное значение.