1. Область определения функции D(x) = R.
2. Функция непрерывна, точек разрыва нет.
3. Пересечение с осью Оу: х=0;

4. Функция непериодическая. Не является ни четной, ни нечетной, т.к., подставляя в формулу -х, мы получаем выражение

.
5. Определяем асимптоты.

Предел бесконечен, следовательно, асимптот не существует.
6. Найдем производную:

Приравняем ее к нулю, найдем критические точки:

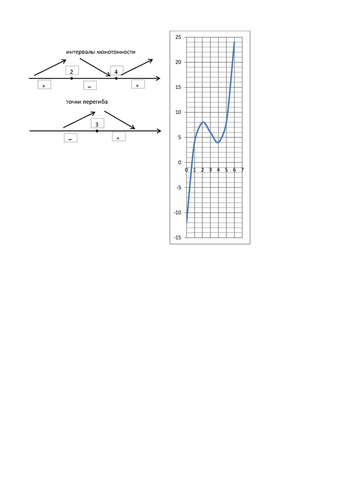
Промежутки возрастания и убывания см. на рисунке.

7. найдем вторую производную:

Точка перегиба (3; 6)
8. Строим график