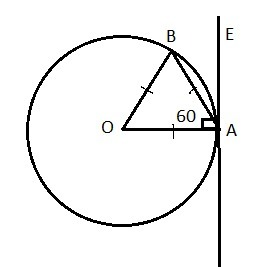
1) Пусть w(O;R) - окружность с центром О и радиусом R, АВ - хорда, АЕ - касательная, проходящая через точку А, и АВ=1/2d.
2) Рассмотрим ΔАОВ - равносторонний, так как ОА=ОВ - радиусы и АВ=1/2d, т.е. АВ=R, значит ∠ОАВ=60°.
2) Свойство касательной: касательная к окружности перпендикулярна радиусу, проведенному в точку касания, т.е. ОА⊥АЕ, значит ∠ОАЕ=90°.
Находим угол между касательной и хордой:
∠ВАЕ=∠ОАЕ-∠ОАВ=90°-60°=30°.
Ответ: 30°.