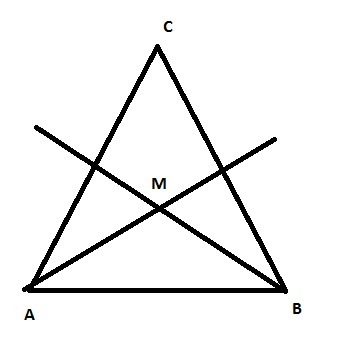
Рассмотрим треугольник АМВ, сумма углов в нем, как и в любом другом треугольнике , 180*
То есть мы можем найти сумму двух неизвестных в этом треугольнике углов.
∠МAВ+∠АBМ=180*-162*
∠МAВ+∠АBМ=18*
Так как данные углы равняются половинам ∠В и ∠А, то и их сумма равна половине.
∠A+∠B=2*(∠МAВ+∠АBМ)
∠A+∠B=2*18
∠A+∠B=36*