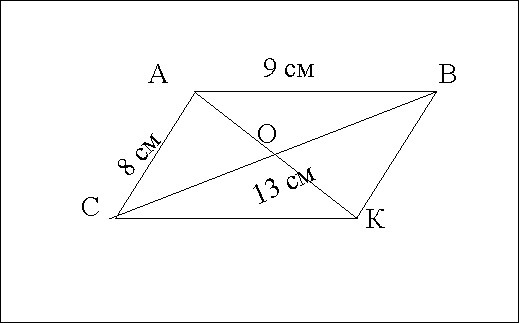
Данный ΔАВС достроим до параллелограмма АВКС и решим через теорему о диагоналях параллелограмма.
Теперь медиана треугольника будет равна половине диагонали получившегося параллелограмма
АО = АК/2
Две стороны треугольника АС и АВ - это боковые стороны параллелограмма АВКС.
Третья сторона треугольника ВС к которой была проведена медиана АО, является второй диагональю получившегося параллелограмма АВКС.
Применим теорему о диагоналях параллелограмма:
сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
2*(a² + b²) = d₁² + d₁²
где
a, b - стороны параллелограмма
d₁, d₂ - диагонали параллелограмма;
отсюда:
d₁² = 2·(a² + b²) - d₂²
а = АС = 8 см
b = АВ = 9 см
d₂ =ВС = 13 см
Ищем d₁ = АК
АК² = 2·(8²+9²)-13² = 2·(81+64)-169 = 2·145-169 = 121
АК = √121 = 11 см
Наша медиана АО = АК/2.
АО = 11 см : 2 = 5,5 см
Ответ: 5,5 см