Сечения шара двумя параллельными плоскостями, между которыми лежит центр шара, имеют площади 144π см, 25π см. Найти площадь поверхности шара, если расстояние между параллельными плоскостями равен 17 см
* * *
Сечение шара плоскостью - круг.
Расстояние между плоскостями равно длине перпендикуляра, опущенного с одной плоскости на другую.
Центр шара и центры сечений параллельными плоскостями лежат на одной прямой.
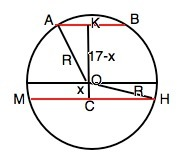
На схематическом рисунке приложения – сечение шара через его центр О и центры сечений.
АК- радиус меньшего сечения, СН - радиус большего сечения, СК - расстояние между центрами сечений, ОА=ОН - радиус шара.
Квадрат радиуса меньшего сечения АК²=S1:π=25
Квадрат радиуса большего сечения СН²=S2:π=144
Обозначим расстояние между центром шара и большим сечением СО=х, тогда между центром шара и меньшим сечением ОК=17-х.
Из ∆ АОК по т.Пифагора
R²=АК²+ОК²
Из СОН
R²=CH²+CO²
Приравняем оба значения R²:
АК²+ОК²=CH²+CO²
25+289-34х+х²=144+х*
34х=170
х=5
R²=ОН²=25+144=169
Формула площади поверхности шара
S=4πR²
S=4π•169=676π см²