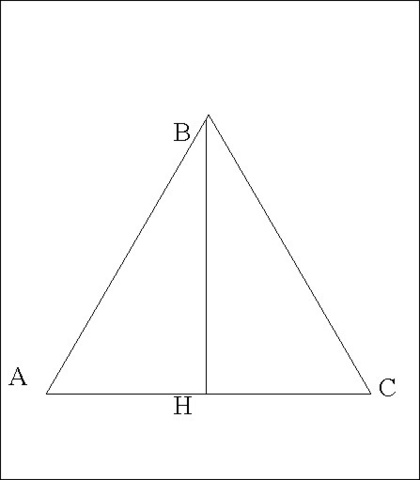
Дано:
ΔАВС
АВ=ВС=АС
ВН⊥АС
ВН =√3
Найти Р ΔАВС
Решение
Пусть х - длина стороны ΔАВС.
В равностороннем треугольнике высота является и медианой, и биссектрисой, и осью симметрии.
Поэтому высота ВН делит АС пополам, т.е. АН = НВ = х/2
ΔАВН - прямоугольный, поэтому применим теорему Пифагора:
АВ² = ВН² + АН²
АВ² - АН² = ВН²
х² - (х/2)² = (4√3)²
х² - х²/4 = 4²√3²
3х²/4=16*3
х²/4=16
х² = 16 · 4
х² = 64
х = √64 = 8 см - сторона ΔАВС
АВ = ВС= АС = 8 см
Р = 3·АВ
Р = 8 см · 3 = 24 см
Ответ: 24 см - периметр.