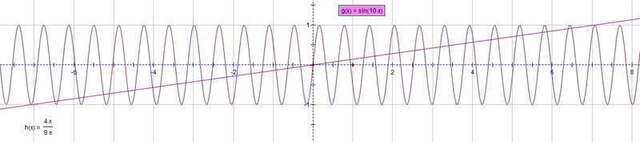
-1 ≤ 4x / (9π) ≤ 1 (синус--функция ограниченная)
-9π ≤ 4x ≤ 9π
-9π/4 ≤ x ≤ 9π/4
-22.5π ≤ 10x ≤ 22.5π
решение уравнения:
10х = (-1)ⁿ * arcsin(4x / (9π)) + πn, n∈Z
по определению -π/2 ≤ arcsin(a) ≤ π/2
1) при х=0 один корень (n=0)
2) n > 0
правая граница: (π/2) + πn ≤ 22.5π
πn ≤ 22.5π - 0.5π
n ≤ 22, n∈Z всего справа от нуля 22 корня))
3) аналогично, слева от нуля тоже 22 корня
Ответ: 45 корней
например, sin(10x) = -1, n = -22
следовательно, 4х/(9π) = -1 ---> х = -9π/4
10х = (-π/2) - 22π = -22.5π ---> x = -2.25π = (-2целых 1/4)π = -9π/4