В параллелограмме ABCD стороны равны 15 и 50 см. С вершины B до плоскости параллелограмма...

Question

В параллелограмме ABCD стороны равны 15 и 50 см. С вершины B до плоскости параллелограмма BM установлено перпендикуляр, равный 18 см. Определите расстояние от точки M до меньшей стороны параллелограмма, если расстояние от точки M до большей стороны равна 30 см.

Answer 1

Расстояние от точки до прямой - длина отрезка, проведенная к ней из этой точки перпендикулярно.

МВ перпендикулярна плоскости параллелограмма, следовательно, любой прямой, проходящей через её основание. 

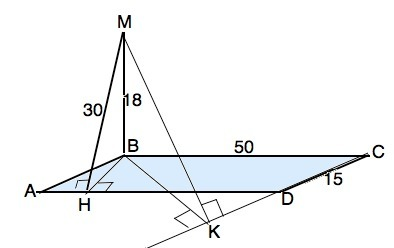
Расстояние  от М до AD - наклонная МН. Её проекция ВН⊥AD по т. о 3-х перпендикулярах ⇒ ВН - высота параллелограмма. 

∆ МВН - прямоугольный.  По т.Пифагора

BH=√(MH²-MB²)=√(900-324)=24 см

S ABCD=BH•AD=24•50=1200 см²

Высота ВК параллелограмма из  его площади:

ВК=1200:15=80 см

 По т. о 3-х перпендикулярах КМ ⊥ CD, является расстоянием от М до  СD - меньшей стороны параллелограмма. 

∆ МВК - прямоугольный. 

По т.Пифагора

МК=√(MB²+BK²)=√(324+6400)=82 см – это ответ. 

---