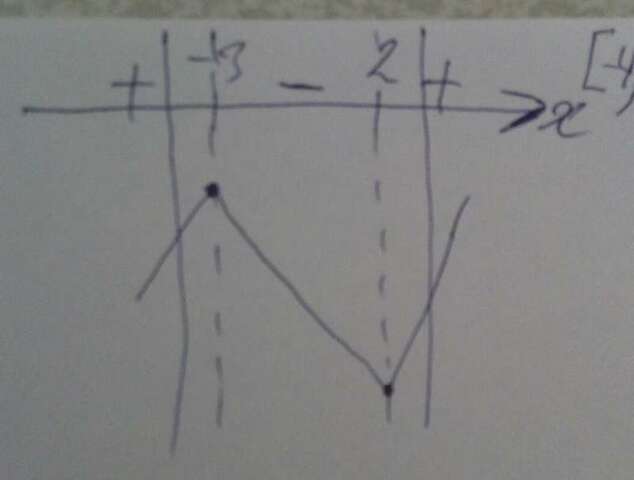
1)D(y)=R.;2)y'=6x^2+6x-36;D(y')=R;y'=0;6x^2+6x-36=0;Разделим на 6, получим:x^2+x-6=0;D=1^2-4*1*(-6)=1+24=25;x1=-1+5/2*1=2;x2=-1-5/2=-6:2=-3. Точки экстремума-это 2 и (-3). Нанесём на числовую ось, определим знаки на промежутках, будет+-+, значит функция сначала возрастает, потом убывает, а потом опять возрастает. И на промежутке [-4;3] найдём f(3)=54+27-108=-27;f(2)=28-72=-44. Значит, fнаиб.[-4;3]=f(3)=-27, а fнаим.[-4;3]=f(2)=-44.Ответ:fнаиб.[-4;3]=f(3)=-27;fнаим.[-4;3]=f(2)=-44.