В равнобедренном треугольника вершина, противоположная основе отдалена от точки...

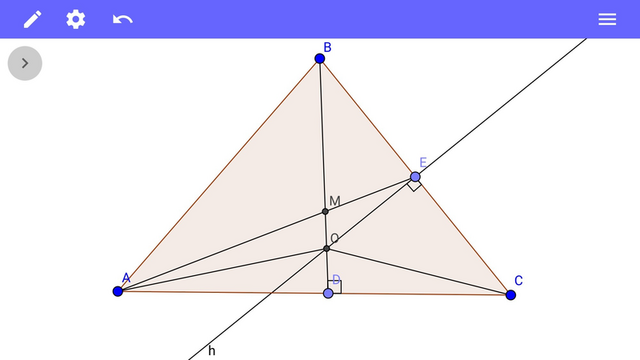
М - точка пересечения медиан. ВМ:МД=2:1 ⇒ ВМ:ВД=2:3.
ВМ=64 см, ВД=3ВМ/2=3·64/2=96 см.

Точка пересечения срединных перпендикуляров - это центр описанной окружности около треугольника. АО=ВО=СО=R=75 см.
ОД=ВД-ВО=96-75=21 см.

В прямоугольном тр-ке АОД АД²=АО²-ОД²=75²-21²=5184,
АД=72 см.
В тр-ке АВД АВ²=АД²+ВД²=72²+96²=14440,
АВ=120 см.

Периметр ΔАВС: Р=2(АВ+АД)=2(120+72)=384 см - это ответ.