1. y=(3-x²)/(x+2) x≠-2
y'=(u/v)=1/v²(u'v-v'u) u=3-x² u'=-2x v=x+2 v'=1
y'=-2x*(x+2)-1*(3-x²)=-2x²-4x-3+x²=-x²-4x-3
x²+4x+3=0 x1=-3 x2=-1
y'=-(x+1)(x+3)
------------- -3-------- -2-------- -1-------
- + -
возрастает монотонно х∈(-3,-2)(-2, -1)
убывает х∈(-∞,-3)∪(-1,∞) точки экстремума -3 и -1
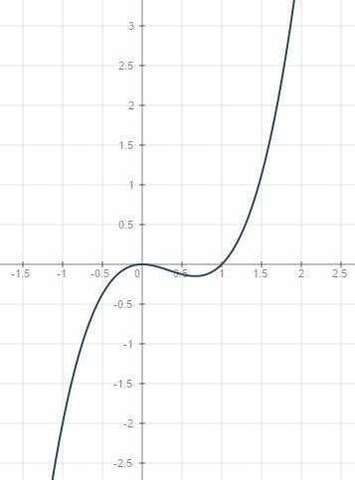
2. y=x³-x² =x²(x-1) корни x=0 x=1
y'=3x²-2x=x(3x-2)
--------------0------------ 2/3-------
+ - + + возрастает - убывает
график приложен
3. y=1/3x³-x²+1 [-1;3]
y'=x²-2x y'=0 x(x-2)=0 x=0 y=1 x=2 y=8/3-4+1=-1/3
x=-1 y=-1/3-1+1=-1/3
x=3 y=27/3-9+1=1
наибольшее 1 наименьшее -1/3
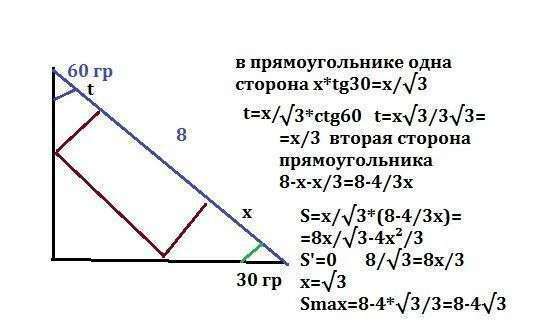
4. решение на приложенном рисунке.
5.sinx>xcosx x∈(0;π/2)
tgx>x
возьмем угол х радиан в 1-ой четверти, площадь сектора единичной окружности при этом равна х/2 (r=1), сектор находится в прямоугольном треугольке с горизонтальным катетом 1 и вторым катетом вертикальным tgx. Площадь треугольника 1*tgx*1/2=tgx/2, из сравнения площадей сектора и треугольника xxcosx
6. надо найти а при которых y'>0 на всей оси х.
y'=5ax²-60x+5(a+9)
a>0 y'>0 при любых а если D<0 и корней нет. D=3600-4*25a(a+9)=<br>=3600-100a²-900a -100a²-900a+3600<0<br>a²+9a-36>0 корни 3 и -12 по т. Виета, мы смотрим только а>0 a∈(3;∞)
а<0 решений нет так как парабола выпуклая вверх не может вся лежать выше оси х.<br>ответ а∈(3,∞)