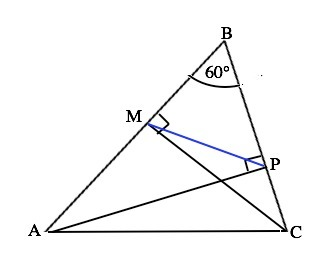
Одна из формул: Площадь треугольника равна половине произведения соседних сторон на синус угла между ними.
В прямоугольном треугольнике АВР гипотенуза АВ=ВР:cos60°=2BP
В прямоугольном треугольнике ВМС гипотенуза ВС=ВМ:cos60°=2ВМ
S ∆ BMP=BM•BP•sin60°:2=10
S ∆ BMP=BM•BP•√3/4=10⇒
BM•BP•√3=40
S ∆ ABC=2BP•2BM•sin60°:2⇒
S ∆ ABC =4 BP•BM√3:4=BM•BP•√3
BM•BP•√3=40 (см. выше)⇒
Площадь ∆ АВС=40 ед. площади.
-------
Заметим, что по первой лемме о высотах (Если в треугольнике ABC нет прямого угла, АА1 и ВВ1 ( здесь AР и СМ ) – его высоты, то ∆ А1В1С подобен ∆ ABC. (здесь ∆ МВР~∆ABC) ∆АВС и МВР подобны с коэффициентом подобия k=ВР:АВ=2
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия, следовательно,
S ∆ ABC:S∆ MBP=k²=4⇒
S ∆ ABC=4 S∆ MBP=40 ед. площади