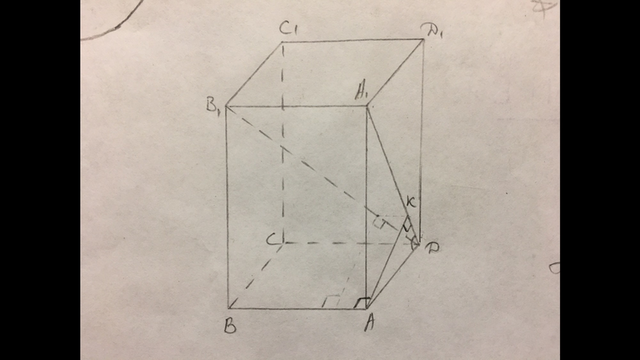
В данной призме АВСД - квадрат со стороной 6 см, АА1=8 см.
Найдём расстояние от стороны основания АВ до не пересекающей её диагонали В1Д.
Расстояние от прямой до не параллельной и не пересекающей её прямой равно расстоянию до параллельной ей плоскости, в которой лежит вторая прямая.
АВ║СД, АВ║А1В1, значит прямая АВ параллельна плоскости А1ДСВ1, В1Д∈А1СВ1.
А1Д∈А1СВ1, АВ∦А1Д, значит расстояние от точки А до прямой А1Д, равно искомому расстоянию.
В прямоугольном треугольнике АА1Д отношение катетов АД и АА1 равно 6:8=3:4, такое же как в египетском треугольнике, значит гипотенуза А1Д=10 см.
АК=h=ab/c=АД·АА1/А1Д=6·8/10=4.8 см - это ответ.