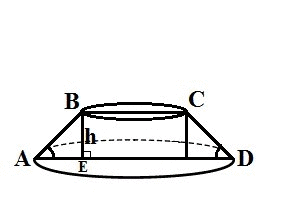
Осевым сечением конуса является равнобедренная трапеция ABCD, где
верхнее основание трапеции BC = 2r = 12 (см)
нижнее основание трапеции AD = 2R = 24 (см)
боковые стороны трапеции AB=CD как образующие
∠BAD = ∠CDA = 45° ⇒ треугольник ABE - прямоугольный равнобедренный, где
высота (h) трапеции BE = AE (как боковые стороны равнобедренного треугольника)
AE = (AD - BC) / 2 (свойство равнобедренной трапеции)
h = (AD - BC) / 2
h = (24 - 12) / 2 = 6 (см)