Оба уравнения в системе представляют собой уравнения окружности.
Центр первой окружности - (0; 0), радиус равен 8;
Центр второй окружности - (0; 1), радиус равен |a|.
Нужно только учесть, что значение параметра a может быть как отрицательным, так и положительным.
Построим первую окружность.
Чтобы система имела единственное решение, обе окружности должны касаться друг друга.
Т.к. центр второй окружности на 1 ед смещён вверх, то для того, чтобы окружности касались, радиус второй должен быть равен |r - 1|, либо |r + 1| (в первой случае окружности будут касаться в точке (8; 0), во второй случае - в точке (-8; 0)).
|r - 1| = 8 - 1 = 7
|a| = 7 ⇒ a = -7 или 7.
|r + 1| = 8 + 1 = 9
|a| = 9 ⇒ a = -9 или 9.
Наименьшее из всех а равно -9.
Ответ: при a = -9.
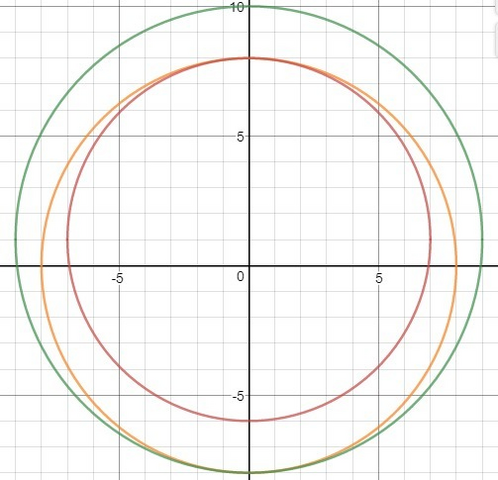
(в приложении красная окружность - x² + y² = 64; оранжевая - x² + (y - 1)² = 49; зелёная - x² + (y - 1)² = 81).