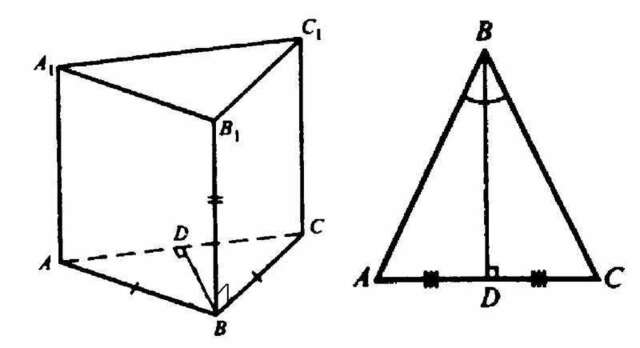
Основаниями призмы являются равные равнобедеренные треугольники, а боковые грани - прямоугольники.
Sполн = 2Sосн + Sбок, где Sполн - площадь полной поверхности призмы, Sосн - площадь основания призмы, Sбок - площадь боковой поверхности призмы.
Sбок = P * h, где P - периметр основания призмы, h - высота призмы, равная длине бокового ребра призмы
P = 10 + 12 + 12 = 34 (см)
Sбок = 34 * 8 = 272 (cм²)
В ранобедренном треугольнике ABC:
Боковые стороны AB = BC = 12 (cм)
Основание AC = 10 см
Высота BD, опущенная на основание равнобедренного треугольника, также является медианой и биссектрисой ⇒ делит AC пополам.
AD = 1/2 * AC
AD = 1/2 * 10 = 5 (cм)
В прямоугольном треугольнике ABD:
Гипотенуза AB = 12 см
Катет AD = 5 см
По теореме Пифагора
AB² = AD² + BD²
BD² = AB² - AD²
BD² = 12² - 5²
BD² = 144 - 25
BD² = 119
BD = √119 (cм)
Sосн = 1/2 * AD * BD
Sосн = 1/2 * 5 * √119
Sполн = 2 * (1/2 * 5 * √119) + 272 = 272 + 5√119 ≈ 282,9 (cм²)