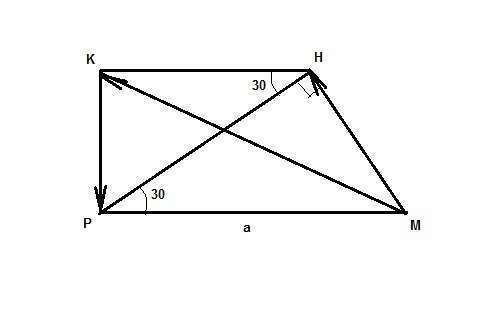
Вот на рисунке эта трапеция со всеми векторами и заданными размерами.
PM = a, PHK = HPM = 30° (накрест лежащие углы), PHM = 90°.
Треугольник MHP - прямоугольный, с углами 30°, 60°, 90°.
По векторам: KP + MK - MH = (MK + KP)- MH = MP - MH = HP
Длина этого вектора |HP| = |MP|*sin HPM = a*sin 30° = a*√3/2