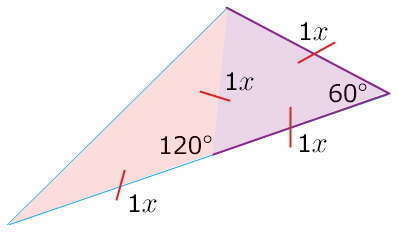
Один угол треугольника (a),
другой угол треугольника (b),
третий угол по условию = (a+b)/2
(a+b) + (a+b)/2 = 180°
(a+b) * (3/2) = 180°
(a+b) = 180° *2 / 3 = 120°
третий угол = (a+b)/2 = 60°
стороны, образующие этот угол, по условию (х) и (2х)
по т.синусов: х / sin(a) = 2x / sin(b)
2*sin(a) = sin(b) и a+b = 120°
2*sin(a) = sin(120°-a)
2*sin(a) = sin(180°-(a+60°)) sin(180°-x) = sin(x)
2*sin(a) = sin(a+60°) sin(30°) = 1/2
2*sin(30°) = sin(30°+60°) sin(90°) = 1
a = 30°; b = 120° - 30° = 90°
другими словами: катет против угла в 30° = половине гипотенузы
можно еще т.косинусов применить (т.к. в 9 кассе тригонометрические преобразования еще не проходят) для третьей стороны:
с² = х² + (2х)² - 2*х*2х*cos(60°)
c² = x² + 4x² - 2x² = 3x²
проверим обратную т.Пифагора:
х² + 3х² = (2х)², т.е. это прямоугольный треугольник))
решение для 7 класса:
на стороне (2х) отложить длину (х), получим равнобедренный треугольник с углом при вершине 60°,
он же будет равносторонним, т.к. оставшиеся два угла равны: (180°-60°)/2 = 60°
внешний угол для этого равностороннего треугольника будет =120° и
вторая часть данного треугольника -это равнобедренный тупоугольный треугольник с углами при основании (180°-120°)/2 = 30°
т.е. мы нашли второй угол данного треугольника = 30°
на третий угол осталось 180°-60°-30° = 90°
это прямоугольный треугольник.