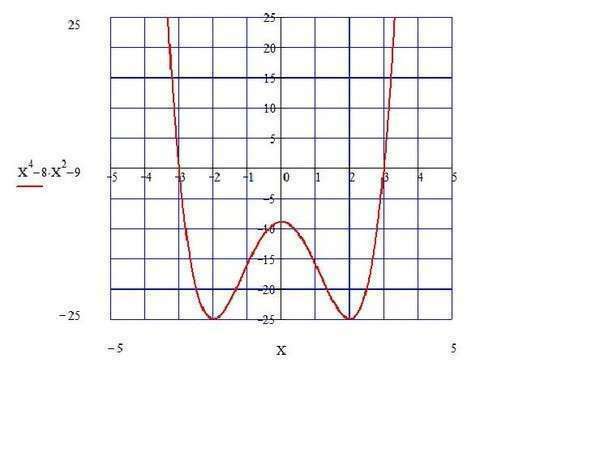
1) исследовать функцию на область определения (определена на всем множестве действительных чисел) |||
2) взять производную по х и исследовать её:
-- там, где она отрицательная, ф-ия убывает|||
-- там, где она положительная, ф-ия возрастает|||
-- там, где она равна нулю, на графике присутствует локальный минимум (х = 0) или максимум (х = 2)|||
-- там, где она не определена, ф-ия имеет разрыв или перелом (таких точек в нашем случае нет) |||
3) взять вторую производную и посмотреть, при каких значениях х она равна нулю. В этом месте у функции будет точка перегиба|||
4) приравнять функцию к нулю и решить получившееся биквадратное уравнение. Получим точки пересечения графика функции с осью х.