В равнобедренном треугольнике ∠С = 90градусов. ** сторонах АС и ВС взяты точки M и N, а...

Question

В равнобедренном треугольнике ∠С = 90градусов. На сторонах АС и ВС взяты точки M и N, а на стороне АВ - точки Р и К так, что четырехугольник MNPK является квадратом. Найдите АВ, если МN = 27.

Answer 1

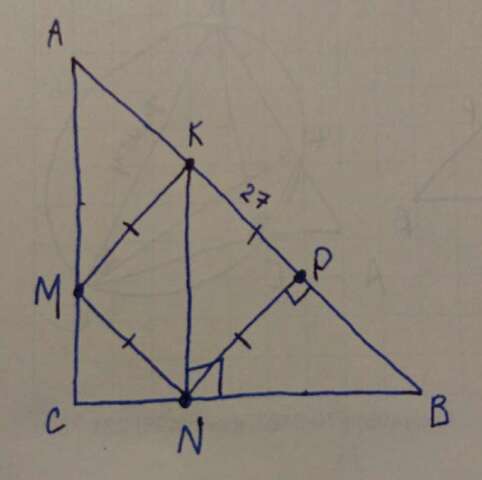
Проведём диагональ KN.

Докажем, что KN ⊥ CB.
KN - диагональ квадрата ⇒ ∠NKP = 1/2 * ∠MKP = 45°
∠CAB = ∠NKB - соответствующие углы ⇒ AC║KN
AC ⊥ CB, AC║KN ⇒ KN ⊥ CB

KN ⊥ CB ⇒ ΔKNB - прямоугольный
∠NKB = 45° (из решения) ⇒ ΔKNB - равнобедренный

∠KPN = 90° (угол квадрата) ⇒ NP ⊥ KB ⇒ NP - высота
Так как ΔKNB - р/б, то NP - медиана ⇒ KP = PB = 27

Аналогично можно рассмотреть диагональ MP и ΔPMA
MK - медиана ⇒ AK = KP = 27

AB = AK + KP + PB = 27 + 27 + 27 = 81

Ответ: 81

---