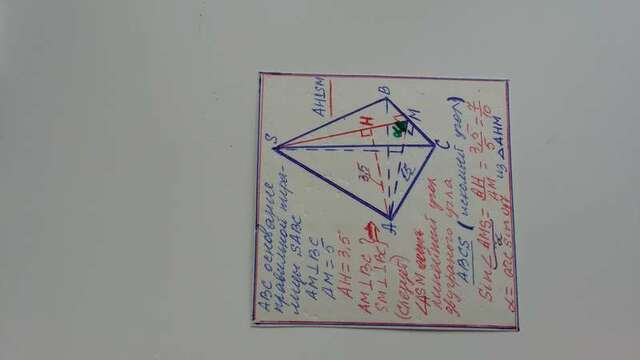
Расстояние от вершины основания правильной треугольной пирамиды до плоскости боковой грани , не содержащей эту вершину , равно 3,5. Высота основания пирамиды равна 5. Найдите синус угла между боковой гранью и основанием пирамиды.
------------------ Рисунок в прикрепленном файле
SABC правильная пирамида
ABC _основание
AB=BC=CA
AM ⊥ BC (BM=CM)
AM = 5
d(A , (SBC) ) = 3,5
---------------
α =∠AMS -? * * * α =∠( ( ABC) , (SBC) ) * **
(линейный угол д
вугранного угла ABCS ;
BC линия пересечения
плоскостей треугольников ABC SBC )
AM ⊥ BC ⇒ BC =CM .Соединим
M
с вершиной пирамиды S .
Получается SM ⊥ BC (т.к. ΔSBC_ равнобедренный: SB=SC) * * *В равнобедренном треугольнике медиана,
проведенная к основанию, является биссектрисой и высотой . * * *
∠AMS _искомый.
Из условий AM ⊥ BC и SM ⊥ BC (BC ⊥ AM , BC⊥ SM) ⇒
BC ⊥ (AMS)
значит и (BCS) ⊥ (AMS), т.к. плоскость BCS проходит через через прямую BC, которая перпендикулярна к плоскости AMS
.
Проведем AH ⊥ SM в плоскости AMS , H ∈ SM. Отрезок
AH и будет
расстояние от точки A до плоскости SBC: AH =
d(A , (SBC) ) = 3,5.
Из ΔAH
M :
sinα =sin(∠AMH)=
sin(∠AMS) =AH /AM =3,5 /5 = 0,7.
α =arcsin(0,7).
ответ : α = arcsin(0,7).
=================
Удачи Вам !