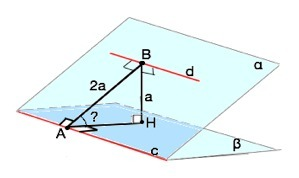
Дано:
α и β – плоскости, с и d- прямые, α пересекает β по прямой с, d||с. d принадлежит α. Расстояние между d и с в два раза больше расстояния от d до β. Найти угол между α и β
Решение:
Плоскости α и β образуют двугранный угол, т.е. фигуру, образованную двумя не принадлежащими одной плоскости полуплоскостями, имеющими общую границу – прямую с ( ребро двугранного угла).
Величина двугранного угла равна величине линейного угла, сторонами которого являются лучи с общим началом на ребре двугранного угла, проведенные в пересекающихся плоскостях и перпендикулярные ребру.
Обозначим вершину линейного угла т.А, АВ⊥с, АН ⊥с, ⇒
∠ВАН - искомый.
Расстоянием между параллельными прямыми (с и d) - это длина перпендикуляра, проведенного из точки на одной прямой (с) на другую (d).
АВ ⊥с по построению, следовательно, АВ⊥d ( по свойству перпендикуляра между параллельными прямыми), ⇒АВ - расстояние между c и d.
Расстояние между плоскостями — длина перпендикуляра, опущенного с одной плоскости на другую. Здесь это длина отрезка ВН.
По условию АВ=2 ВН. По т. о 3-х перпендикулярах НА⊥с. Треугольник ВАН - прямоугольный,
sin∠BAH=ВН:2ВH=1/2. Это синус 30°. Искомый угол=30°