1) Эти два треугольника – прямоугольные, по условию у них
есть прямой угол. Тогда сумма двух оставшихся углов 90°, так как сумма
всех углов любого треугольника 180°, а один угол уже есть, он 90°. 180°-90° – это на два оставшихся.
Теперь что получается? Угол АДС=50°, тогда в треугольнике АСД
другой острый угол 90°-50=40°. Удача! Во втором
треугольнике тоже есть угол 40° по условию. Итак, в этих двух
прямоугольных треугольниках есть равные острые углы. Кроме того, у них сторона
АД – общая. Это гипотенуза. Тогда треугольник АВС и треугольник АСД равны по
острому углу и гипотенузе.
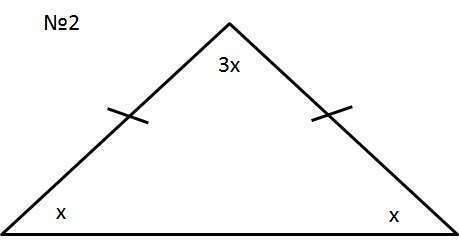
2) Треугольник равнобедренный, поэтому углы при основании
равны. Пусть угол при основании будет х градусов, тогда второй угол при
основании тоже х градусов. По условию угол между боковыми сторонами в три раза
больше, то есть, 3х.
Один угол х
Второй угол х
Третий угол 3х
Сумма углов треугольника 180°.
х+х+3х=180°
5х=180°
х=36°
Тогда углы при основании по 36° градусов.
Угол между боковыми сторонами 3·36°=108° градусов.
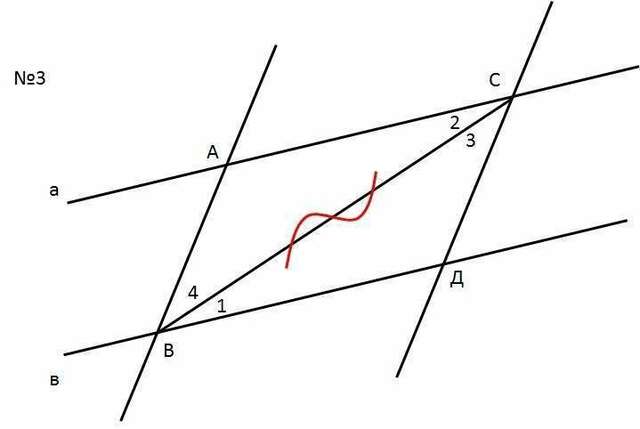
3) Чертёж на фотографии. Проведём ВС, соединив точки В и Д.
Получились треугольники АСВ и ВДС.
Они равны по стороне и двум прилежащим к ней углам:
сторона ВС у них общая
угол 1 равен углу 2, они накрест лежащие при параллельных
прямых АС и ВД и секущей ВС
угол 3 равен углу 4, накрест лежащие при параллельных АВ и
СД и секущей ВС.
Раз треугольники равны, то соответствующие стороны в них
равны, то есть, АС=ВД.