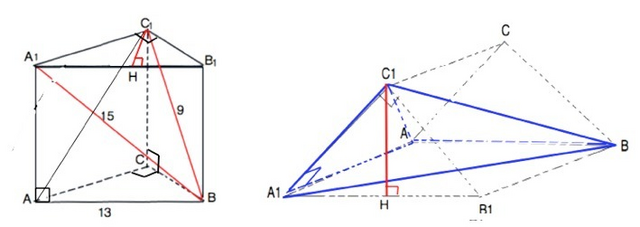
а) Для доказательства нужно найти сторону А1С1 и проверить треугольник на соответствие т.Пифагора.
Призма прямая, ⇒все её ребра перпендикулярны основаниям.
• Из ∆ АА1В по т.Пифагора
АА1=√(A1B²-AB²)=√56
BB1=CC1=√56
• Из ∆ С1СВ по т.Пифагора
ВС=√(BC1²-CC1*)=√(81-56)=√25=²
• Стороны ∆ АВС из троек .Пифагора с отношением 5:12:13 ⇒ можно обойтись без вычислений. АС=12 ( проверьте по т.Пифагора)
А1С1=АС=12
А1В²-С1В²=225-81=144 Получаем А1С1=12, к тому же отношение сторон ВС1:А1С1:А1В=3:4:5 - отношение сторон прямоугольного (египетского) треугольника. Доказано.
–––––––––––––––––––––––––––––
б)Формула объёма пирамиды
V=S•h:3
Площадь основания АВА1 равна половине площади большей боковой грани призмы АВВ1А1 (диагональ грани делит её пополам).
S=AA1•AB:2=√56•13=2√14•13:2=√14•13
Высотой пирамиды является перпендикуляр из вершины С1 опущенный на плоскость основания.
Перпендикуляр из вершины С1 на плоскость АВВ1А1, содержащую плоскость основания пирамиды, лежит в плоскости верхнего основания призмы А1С1В1.
С1Н=А1С1•sin∠A1.
sin∠A1=C1B1:A1B1=5/13
C1H=12•5/13=60/13

------
На втором рисунке приложения призма для большей наглядности "уложена" на большую грань, содержащую основание пирамиды.