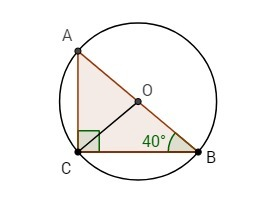
Пусть дан ΔАВС, ∠С=90°, ∠В=40°, О - центр опис. окр.
∠А = 90°-∠В = 90 - 40 = 50°
Против меньшего угла лежит меньшая сторона, значит АС<ВС и <br>∠АОС < ∠СОВ, следовательно нужно найти градусную меру ∠АОС.
В прямоугольном треугольнике центр опис.окр. лежит на середине гипотенузы, значит, СО = АО (радиусы) ⇒ ΔАОС - равнобедренный.
В равнобедр. Δ углы при основании равны ⇒ ∠АСО = ∠САО = 50°
∠АОС = 180-(∠АСО+∠САО) = 180 - 50*2 = 80° (сумма углов Δ = 180°)
Ответ: 80°