ОчЕнЬ пРоШу РеШиТь!!))))))

Question

ОчЕнЬ пРоШу РеШиТь!!))))))

---

Answer 1

Пусть дана трапеция АВСД, где КЕ =1 середина ВС и  МР=11 середина боковых сторон АВ и СД. Продолжим боковые стороны до пересечения в точке Т, тогда угол АТД =90 градусам. Обозначим половину ВС через х , а половину  АД чрез у, тогда получим систему уравнений с двумя переменными  х+у=11 и у-х=1 , решив найдем х=5 и у=6 , соответственно ВС=10 и АД=12

Comments

уйцуйцуйцуйцуйцуйцуйцу

---

Тут нужно учитывать , то что в прямоугольном треугольнике медиана проведенная из вершины прямого угла равна половине гипотенузы, т.е. ТК=1/2ВС и ТЕ=1/2АД

Answer 2

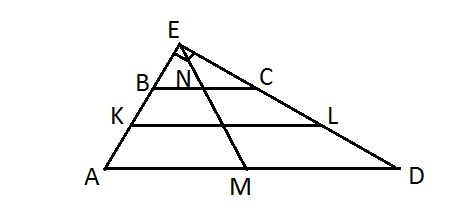
1) Пусть ABCD - трапеция, AD║AC - основания, ∠A=85°, ∠D=5°, K, L, M, N - середины сторон, KL=11, NM=1.
2) Продолжим стороны AB и CD до пересечения в точке Е.
ΔAED - прямоугольный, так как ∠Е=180°-(85°+5°)=180°-90°=90°.
ЕМ - медиана прямоугольного треугольника, проведенная из прямого угла, поэтому она равна ЕМ=1/2*AD.
EN - медиана прямоугольного треугольника, проведенная из прямого угла, поэтому она равна EN=1/2*ВС.
Отсюда MN=EM-EN=1/2AD-1/2BC=1/2(AD-BC)=1.
3) KL - средняя линия трапеции ABCD, KL=1/2(AD+BC)=11. 
Получаем систему уравнений с двумя неизвестными:
(1) 1/2(AD-BC)=1,
(2) 1/2(AD+BC)=11;
(1) AD-BC=2,
(2) AD+BC=22;
Решаем методом сложения:
2AD=24;
AD=24/2=12.
BC=AD-2=12-2=10.
Ответ: 12; 10.

---