Сначала хотел написать, что из условия неясно, на какой стороне отмечена точка H, а потом понял, что это неважно: расстояния равны до обеих точек)
Для решения этой задачи будем использовать две теоремы:
а) Диагонали параллелограмма в точке пересечения делятся пополам.
б) Центр описанной окружности в прямоугольном треугольнике лежит на середине гипотенузы (или, говоря по-другому, центр гипотенузы равноудалён от всех вершин).
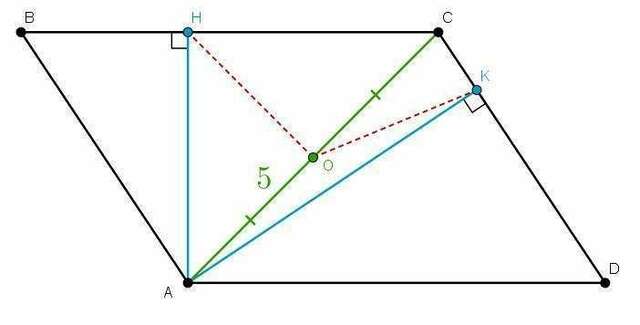
1. Строим чертёж. O — точка пересечения диагоналей. Голубым цветом отмечены высоты, зелёным — диагональ, красным пунктиром — искомое расстояние.
2. Рассмотрим прямоугольный треугольник AHC. Точка О лежит на середине стороны AC (теорема "а"), то есть гипотенузы. Следовательно, это центр описанной окружности (теорема "б"), а значит, точка O равноудалена от всех вершин: HO=AO=OC=2.5.
3. Рассмотрим теперь прямоугольный треугольник CKA. По такой же логике получаем, что OK=AO=OC=2.5.