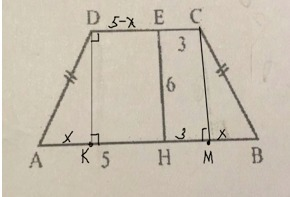
ABCD- равнобедренная трапеция. ЕН перпендикулярна АВ, ЕС=3 см, ЕН=6 см, АН=5 см. S=?
Опустим из тупых углов трапеции высоты DK и CM на основани АВ.
Так как трапеция равнобедренная, углы при основании АВ равны, и
∆ ADK = ∆BMC.
Примем АК=МВ=х
Тогда DE=KH=5-x, BH=3+x
Площадь трапеции равна произведению её высоты на полусумму оснований.
S=EH•(DE+EC+AH+HM+BM):2
S=6•(8-х+8+х):2=48 см²