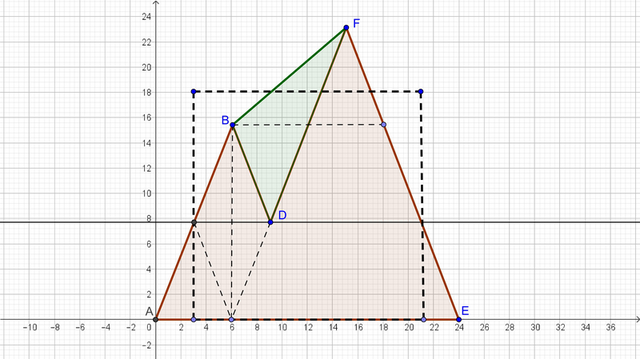
Проведём горизонтальный отрезок из середины АВ в точку Д.
А также из точки В до EF.
Из точки В опустим перпендикуляр на АЕ. Основание этого перпендикуляра соединим с точкой Д.
Теперь видно, что четырёхугольник ABFE состоит из равнобокой трапеции ABB1E и треугольника BFB1.
Если принять расстояние от АЕ до середины АВ за h, то высота трапеции равна 2h. высота треугольника BFB1 равна h.
Отрезок на уровне h, соединяющий АВ и FЕ, - это средняя линия трапеции.
Так ка площадь четырёхугольника равна 324 см², то примем за основу квадрат 18*18 = 324 см².
Пусть средняя линия трапеции равна 18 см.
Из подобия треугольников (DF равно двум половинам АВ), то средняя линия разделится в отношении 1:2, то есть 6:12 см.
Треугольники равнобедренные, поэтому 6 делим пополам, основание трапеции получим равным 18+2*3 = 24 см.
Аналогично верхнее основание равно 18-2*3 = 12 см.
Площадь ABFE равна: S = ((12+24)/2)*2h + (1/2)12*h = 36h+6h = 42h.
Так как S = 324 см², то h = 324/42 = 162/21 ≈
7,714286 см.
Площадь четырёхугольника без искомого треугольника равна:
S1 = 3*(1/2)*6*h + (1/2)18*3h = 9h+27h = 36h.
Отсюда получаем площадь ВДЕ:
S(ВДЕ) = 42h - 36h = 6h = 6*162/21 =
324/7 ≈ 46,28571 см².