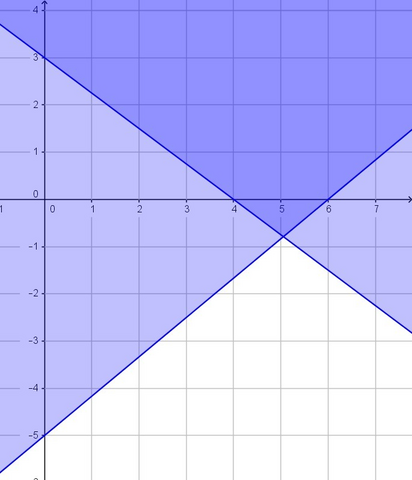
Построим области на координатной плоскости, отвечающие решениях каждого из неравенств.
Первое неравенство 3x + 4y >= 12 - полуплоскость, ограниченная прямой 3x + 4y = 12. На границе лежат, например, точки (4, 0) и (0, 3). Проводим прямую через две точки, неравенству удовлетворяют точки, лежащие выше прямой.
Со вторым неравенством разбираемся так же. На границе лежат точки (6, 0) и (0, -5), решение неравенства - полуплоскость над прямой.
Решение системы неравенств - множество точек, для которых выполняются оба неравенства. На рисунке область, соответствующая этому множеству, изображена более темным цветом.
Можно решение записать и формулами. Найдем точку пересечения прямых, ограничивающих множества решений неравенств.
3x + 4y = 12 | *3
5x - 6y = 30 | *2
9x + 12y = 36
10x - 12y = 60
Складываем равенства:
19x = 96
x = 96 / 19
Решение - y >= 3 - 3x/4 при x <= 96/19 и y >= 5x/6 - 5 при x > 96/19