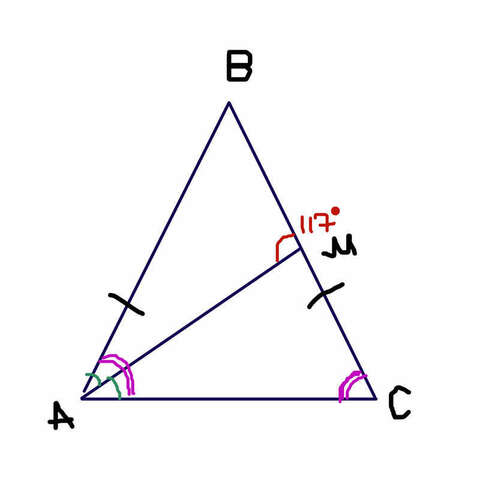
Розглянемо трикутник АМС. Сумка кутів трикутника дорівнює 180°, тоді ∠МАС+∠МСА+∠АМС=180°.
Сума суміжних кутів дорівнює 180°. Кути АMВ i AMC суміжні. Відомо, що ∠АМВ=117°, отже ∠АМС=180°-117°=63°
Бісектриса ділить кут навпіл отже ∠ВАС= ∠ВАМ+ ∠МАС=2∠МАС.
Трикутник АВС рівнобедрений тому кути при основі рівні тобто ∠ВАС=∠ВСА, отже оскільки ∠ВАС=2∠МАС, то і ∠ВСА=2∠МАС
Звідси ∠МАС+2∠МАС+63°.=180°.
3∠МАС=180°-63°
3∠МАС=117°
∠МАС=39°
∠ВАС=∠ВСА= ∠ВАМ+ ∠МАС=2∠МАС=2*39°=78°
∠АВС=180°-78°-78°=24°- за т. про суму кутів трикутника.
Відпповідь: ∠АВС=24°, ∠ВАС=∠ВСА=78°