Для начала найдем производную функции
y'=(x^2)'*ln x+x^2*(ln x)'
y'=2x*ln x+x^2*(1/x)
y'=2x*ln x+x
Что бы найти экстремумы приравняем производную к нулю
2x*ln x+x=0
x(2*ln x+1)=0
2*ln x+1=0 x=0 это первый корень
2*ln x=-1
ln x= -1/2
x= e^(-1/2)
x=1/√e
получаем два корня x=0 и x=1/√e
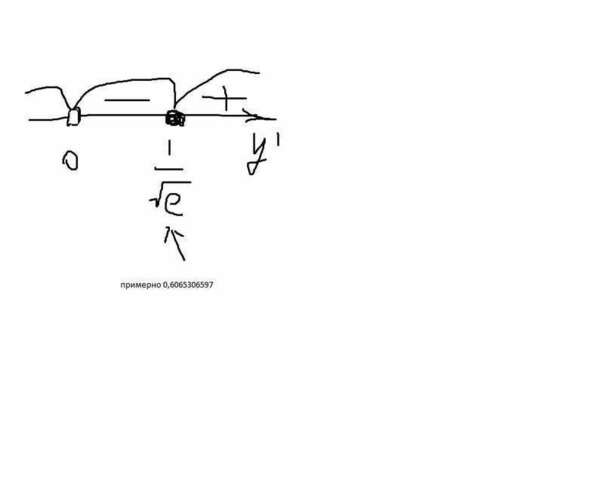
Начертим график и посчитаем интервалы монотонности
Так как у нас ln x то область определения y' x>0 по этому за ее пределами мы знаки не считаем
Исходя из графика видно, что при x э (0;1/√e) функция убывает т.к. производная на данном интервале отрицательная, а на интервале (1/√e;+∞) функция возрастает т.к. производная на данном интервале положительная.
У нас имеется одна точка экстремума x=1/√e, и она является точкой минимума так как в ней производная меняет знак с - на +, то есть функция перестает убывать и начинает расти.