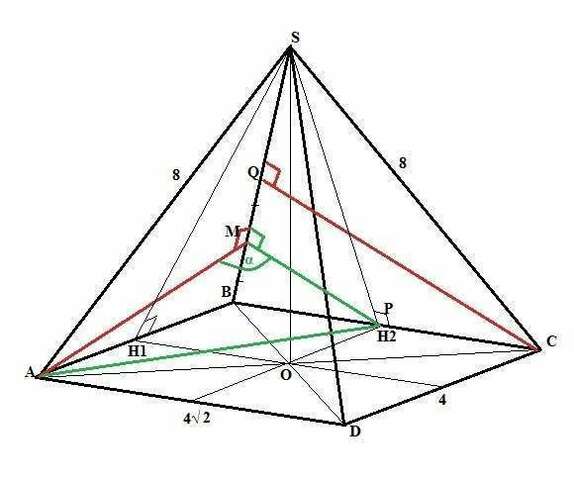
Боковые ребра пирамиды равны (так как вершина проецируется в центр основания). Значит АS=BS=CS=DS=8.
Грани - равнобедренные треугольники.
а) Рассмотрим равнобедренный треугольник АSВ. В нем высота SH1, опущенная на основание AB по Пифагору равна √60.
Соответственно, площадь грани АSB равна Sasb= 2√60.
Тогда АМ (высота к боковой стороне BS) равна АМ=2Sasb/SB или
АМ=4√60/8=√60/2. МВ по Пифагору равно МВ=√(АВ²-АМ²) или
МВ=√(16-60/4)=1.
Точно также в треугольнике ВSC имеем:
SH2=√(64-8)=√56.
Sbsc=2√2*√56=2√112.
CQ=2Sbsc/SC или CQ=√112/2. Тогда
BQ=√(BC²-CQ²) или BQ=√(32-112/4)=√(16/4)=2.
итак, доказано, что BQ=2*BM, то есть точка М - середина BQ.
б) Цитата:"Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. Таким образом, чтобы измерить двугранный угол, можно взять любую точку на его ребре и перпендикулярно ребру провести из неё лучи в каждую из граней".
Возьмем на ребре BS точку М и проведем из нее в гранях ASB и CSB
перпендикуляры. Один из них нам уже знаком - это отрезок АМ.
Второй - отрезок МР, который будет параллелен отрезку СQ и равен его половине (так как МР - средняя линия треугольника BQC, поскольку точка М - середина отрезка BQ - доказано выше). По Пифагору: АР=√(АВ²+ВР²) или АР=√(16+8)=2√6.
Тогда по теореме косинусов из треугольника АМР искомый угол АМР равен:
Cosα = (b²+c²-a²)/2bc. Или
Cosα = (АМ²+МР²-АР²)/2*АМ*МР.
Cosα = (60/4+112/16-24)/2*(√60/2)*(√112/4)=-8/81,97=-0,097.
Угол равен arccos(-0,097) или α≈95,57°