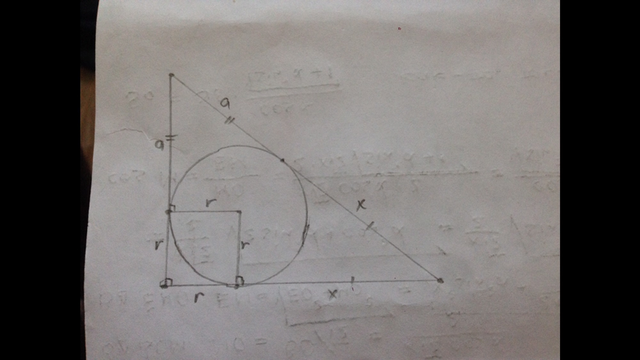
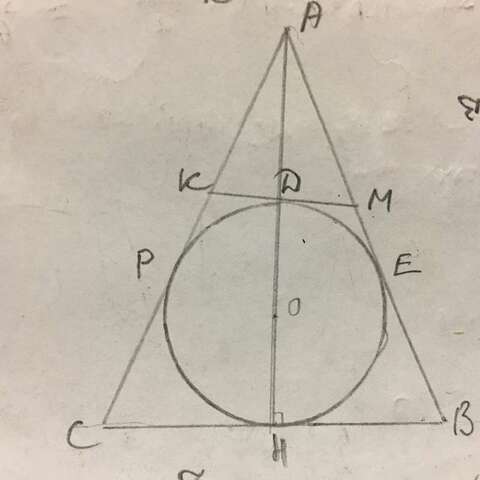172. Касательные к окружности, проведённые из одной точки равны.
На рисунке символами а, х и r отмечены равные отрезки.
По условию отрезки гипотенузы а=3 см и х=10 см.
Периметр Р=2а+2х+2r ⇒ r=(P-2(a+x))/2=(P-2c)/2, где с - гипотенуза.
с=3+10=13 см,
r=(30-2·13)/2=2 см - это ответ.
173. АВ=АС=10 см, Р(АМК)=14 см.
АР=АЕ, КР=КД, МД=МЕ.
Р(АМК)=АМ+АК+КД+МД=АК+АМ+КР+МЕ=АР+АЕ ⇒ АР=АЕ=Р(АМК)/2=14/2=7 см.
СР=АС-АР=10-7=3 см.
Центр вписанной окружности лежит на пересечении биссектрис. Так как ΔАВС равнобедренный, то биссектриса АО является высотой и медианой, значит центр вписанной окружности лежит на высоте АН. Радиус ОН⊥ВС, АН - медиана, значит СН=ВН.
СР=СН=ВЕ=ВН=3 см, АР=АЕ=7 см, отсюда Р(АВС)=2АР+4СР=2·7+4·3=26 см - это ответ.