Sin² A + cos² A = 1
cos²A = 1 - sin²A
cos²A = 1 - (2√6/5)² = 1 - (24/25) = 25/25 - 24/25 = 1/25
cos A = √(1/25) = 1/5
-------------------------------------------------------------------------------------------------------------
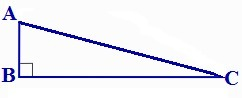
Если решать геометрически, то синус угла А является отношением противолежащего углу А катета BC к гипотенузе AC. Косинусом угла А является отношение прилежащего к углу А катета AB к гипотенузе AC.
Если прилежащий катет относится к гипотенузе как 2√6 : 5, для вычисления синуса и косинуса угла А можно принять длину прилежащего катета = 2√6, а гипотенузу = 5. Т.к. прямоугольный треугольник с иными длинами сторон, но с таким же синусом того же угла будет подобен треугольнику с длиной прилежащего к углу катета = 2√6 и гипотенузой = 5. У подобных треугольников стороны одного пропорциональны сходственным сторонам другого, а их соответствующие углы равны.
BC = 2√6 см
AC = 5 см
по теореме Пифагора
BC² + AB² = AC²
(2√6)² + AB² = 5²
24 + AB² = 25
AB² = 1
AB = 1 (cм)
cos A = AB / AC
cos A = 1/5