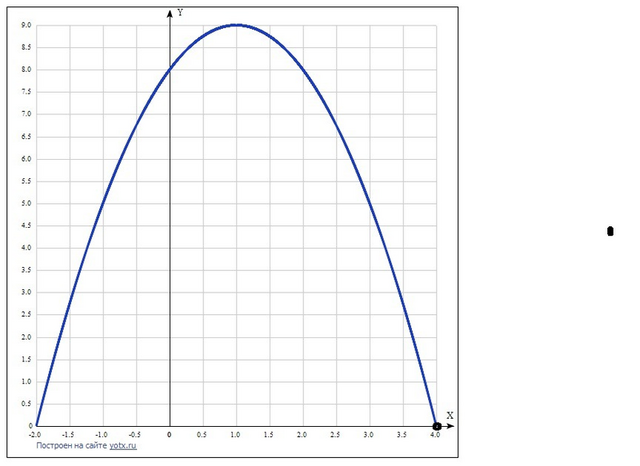
Дана функция у = (x³ -6x² + 32)/(4 - x).
Если х не равен 4, то числитель можно разделить на знаменатель и получим квадратичную функцию у = - x² + 2x + 8.
График её - парабола ветвями вниз.
Заданное условие выполняется, когда прямая y = а является касательной к графику в вершине параболы.
Хо = -в/2а = -2/(2*(-1)) = 1.
Отсюда имеем один из ответов: а = у(х=1) = -1+2+8 = 9.
Так как заданная функция не существует в точке х = 4, то прямая у = 0 пересекает график только в точке х = -2.
Второй ответ: а = 0.