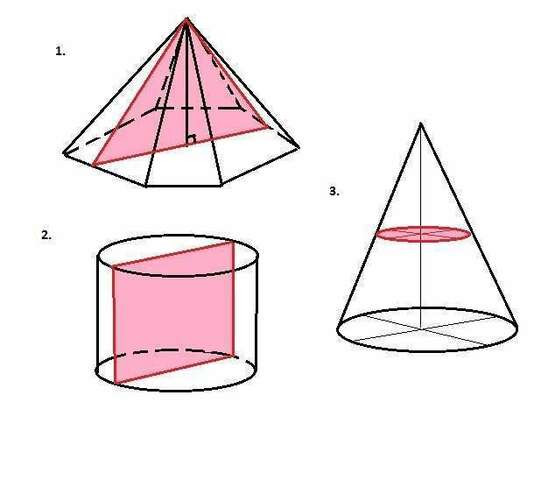
Ответы:
1. При сечении пирамиды плоскостью, перпендикулярной основанию и проходящей через вершину, линия пересечения плоскости сечения и плоскости, содержащей основание, проходит через точку основания высоты пирамиды и через две противоположные точки, находящиеся на линиях пересечения двух противоположных боковых граней пирамиды. То есть плоскость сечения проходит через три общих с пирамидой точки, а фигура, состоящая из трех прямых, пересекающихся в трех точках - треугольник.
Ответ: а) - треугольник
2. Плоскость сечения пересекает параллельные плоскости по параллельным прямым. Значит линии пепесечения оснований цилиндра с плоскостью сечения параллельные и равные отрезки (так как основания цилиндра - параллельные круги равных диаметров, а образующие цилиндра перпендикулярны основаниям). Фигура сечения - прямоугольник по определению, так как имеет пары параллельных и равных сторон.
Ответ: а) - прямоугольник
3. Сечение конуса плоскостью, параллельной основанию, пересекает конус по линии, параллельной основанию, то есть по линии, все точки которой равноудалены от линии основания. Следовательно, плоскость сечения - круг, подобный кругу основания.
Ответ: г) - круг