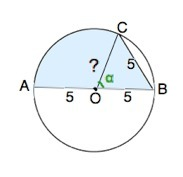
Обозначим диаметр АОВ, хорду - СВ. Искомая площадь равна сумме площадей сектора АОС и треугольника ВОС.
R=10:2=5 см
Так как хорда равна радиусу, ∆ ВОС правильный. Его площадь
по формуле S=a²√3/4=25√3/4
∠АОС=120°( смежный ∠ВОС правильного треугольника, равному 60°)
360°:120°=3⇒
Сектор АОС=1/3 круга
S(AOC)=πr²/3=25π/3 см²
S(ABC)=25√3/4+25π/3=25(3√3+4π)/12 см²