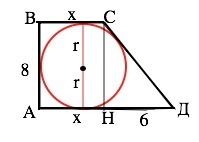
Обозначим трапецию АВСD. АВ перпендикулярна ВС и АD. Диаметр окружности, вписанной в трапецию, равен её высоте. Так как трапеция прямоугольная, ее высота равна стороне АВ=2r=8(см)
Примем меньшее основание равным х.
Опустим из вершины С высоту СН на большее основание. Тогда АН=ВC=х, АD=х+6, НD=6.
По т.Пифагора из ∆ СНD
СD=√(CH²+HD²)=√(64+36=10 (см)
Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы его противоположных сторон равны.
Трапеция - четырехугольник⇒
ВС+АD=АВ+СD
х+х+6=8+10
2х=12
х=6⇒ BC=6 см, AD=12 см
Площадь трапеции равна произведению высоты на полусумму оснований.
S=8•((6+12):2=72 (см²)