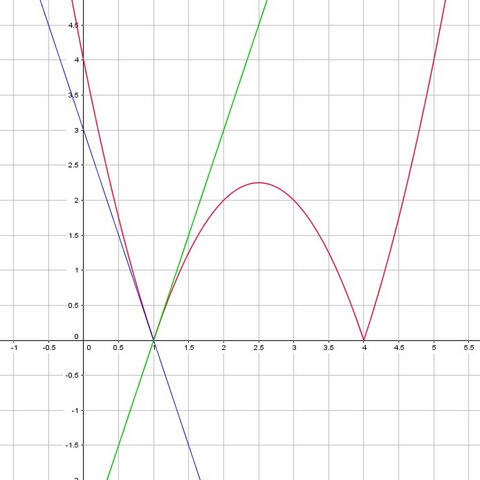
Доказательство прицеплено в первой картинке. Если нужно совсем наглядное объяснение, то оно во второй картинке с графиками: график функции f(x) (красная линия), в точке х=1 имеет "зубец" - что означает, что в этой точке есть две различных касательных к графику (синяя и зеленая прямые). А когда в какой-то точке график функции имеет не единственную касательную, то в этой точке функция не имеет производной. Аналогично, кстати и с точкой х=4.