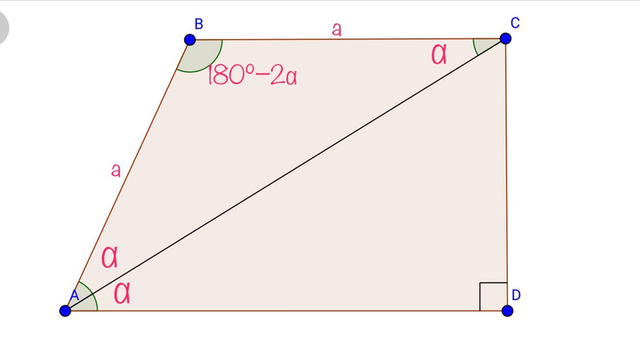
∠АСВ=∠САД=α как накрест лежащие, ∠ВАС=∠ВСА=α как лежащие у основания равнобедренного треугольника, значит ∠ВАД=2α.
∠АВС=180-∠ВАД=180-2α.
S(АВС)=a²·sin(180-2α)/2=(a²·sin2α)/2.
По теореме косинусов АС²=АВ²+ВС²-2АВ·ВС·cos(180-2α),
AC²=a²+a²+2a²·cos2α=2a²(1+cos2α).
S(АСД)=(АС²·sin2α)/4=(a²·(1+cos2α)·sin2α)/2.
S(АВСД)=S(АВС)+S(АСД)=а²·sin2α·(2+cos2α)/2 - это ответ.