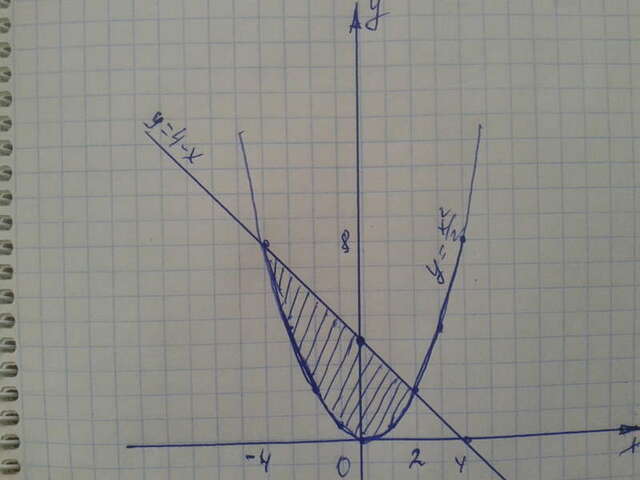
Y=x²/2 y=4-x V=?
x²/2=4-x |×2
x²=8-2x
x²+2x-8=0 D=36
x₁=-4 x₂=2
V=π₋₄∫²((4-x)²-(x²/2)²)dx=π₋₄∫²(16-8x+x²-x⁴/4)dx=π(-x⁵/20+x³/3-4x²+16x) |₋₄²=
=π((-2⁵/20+2³/3-4*2²+16*2)-(-(-4)⁵/20+(-4)³/3-4*(-4)²+16*(-4)))=
=π((-32/20+8/3-16+32-(1024/20-64/3-64-64))=
=π(-8/5+8/3+16-256/5+64/3+128)=π(-264/5+72/3+144)=π*1728/15=576π/5.
Ответ: V=576π/5≈≈361,9 куб. ед.