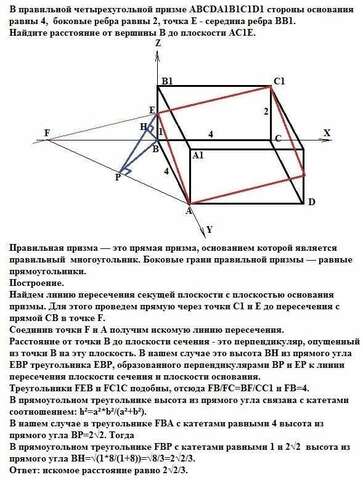
В правильной четырехугольной призме АВСDA1B1C1D1 стороны основания равны 4, боковые ребра равны 2, точка Е - середина ребра ВВ1.
Найдите расстояние от вершины В до плоскости АС1Е.
Правильная призма — это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы — равные прямоугольники.
Построение.
Найдем линию пересечения секущей плоскости с плоскостью основания призмы. Для этого проведем прямую через точки С1 и Е до пересечения с прямой СВ в точке F.
Соединив точки F и А получим искомую линию пересечения FA.
Расстояние от точки В до плоскости сечения - это перпендикуляр, опущенный из точки В на эту плоскость. В нашем случае это высота ВН из прямого угла ЕВР треугольника ЕВР, образованного перпендикулярами ВР и ЕР к линии пересечения плоскости сечения и плоскости основания.
Треугольники FЕB и FС1С подобны, отсюда FB/FC=BF/CC1 и FB=4.
В прямоугольном треугольнике высота из прямого угла связана с катетами соотношением: h²=a²*b²/(a²+b²).
В нашем случае в треугольнике FBA с катетами равными 4 высота из прямого угла ВР=2√2. Тогда
в прямоугольном треугольнике FBР с катетами равными 1 и 2√2 высота из прямого угла ВН=√(1*8/(1+8))=√8/3=2√2/3.
Ответ: искомое расстояние равно 2√2/3.
Второй способ - метод координат.
Пусть начало координат в точке В.
Итак, у нас есть плоскость, проходящая через три точки А(0;4;0), Е(0;0;1) и С1(4;0;2) и есть точка В(0;0;0), через которую проходит перпендикуляр к плоскости. Надо найти длину этого перпендикуляра от точки В до плоскости АЕС1.
Решение.
Для составления уравнения плоскости используем формулу:
|x-xA xЕ-xA xC1-xA|
|y-yA yЕ-yA yC1-yA| = 0.
|z-zA zЕ-zA zC1-zA|
Подставим данные трех наших точек:
|x-0 0-0 4-0| |x 0 4|
|y-4 0-4 0-4| = 0. Или |y-4 -4 -4| = 0.
|z-0 1-0 2-0| |z 1 2|
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
|-4 -4| | 0 4| | 0 4|
х*| 1 2| - (y-4)*| 1 2| +z*|-4 -4| =0. Отсюда
х(-8+4)-(y-4)(0-4)+z(0+16)=0.
-4x+4y-16+16z=0.
x-y-4z+4=0 Это уравнение плоскости сечения в виде Аx+By+Cz+D,
где А=1, B=-1, C=-4, D=4.
Если задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(Mx; My; Mz) до плоскости можно найти, используя следующую формулу:
d=|A*Mx+B*My+C*Mz+D|/√(A²+B²+C²) или в нашем случае:
d=|0+0+0+4|/√(1+1+16)=4/√18=4/(3√2)=2√2/3.
Ответ: искомое расстояние равно 2√2/3.