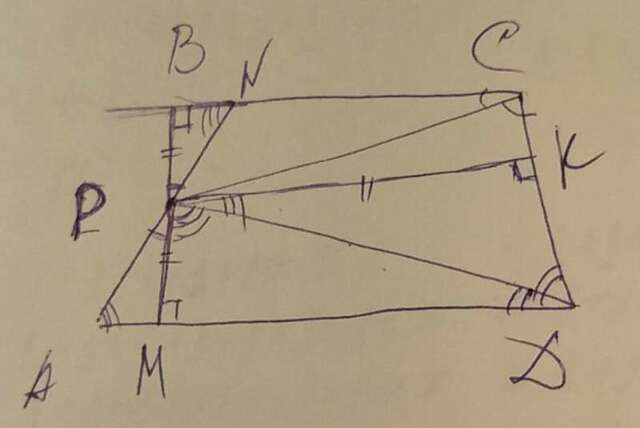
Не понятно какая точка равноудалена: Е или Р, и где находится точка Р тогда.
Расстояние от точки до прямой это перпендикуляр, значит PB перпендикулярна ВС, РМ перпендикулярна AD, PK перпендикулярна CD и надо доказать что PB=PM=PK.
1. Рассмотрим четырёхугольник PKDM.
В нём два треугольника, образованные биссектриссой DP. Угол KPD=90-уголKDP (по свойству но сумме углов прямоугольного треугольника). Угол DPM=90-уголMDP. Но углы KDP и MDP равны, значит углы KPD и DPM равны.
2. Прямоугольный треугольники KPD и MPD равны по острым углам и гипотенузе, следователь PK=PM.
3. Аналогично доказывается что в четырёхугольнике PBCK треугольники CKP и СВР равны и PB=PK.
РВ=РК=РМ ч.т.д.