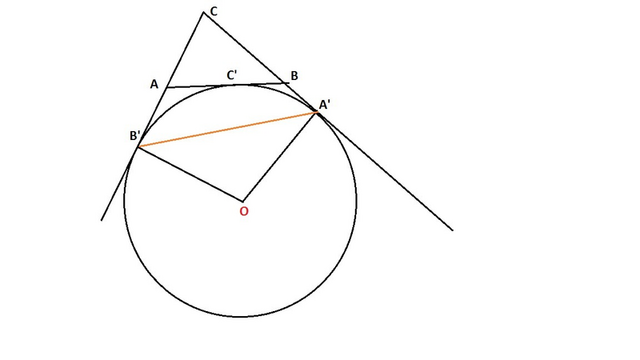
Обозначим центр данной вневписанной окружности точкой О. Проведём радиусы в точки касания (в точки B' и A').
Рассмотрим ΔOB'A'.
OB' = OA' = R ⇒ ΔOB'A' - равнобедренный и тогда ∠OB'A' = ∠OA'B'.\
Т.к. радиус, проведённый в точку касания, перпендикулярен касательной, то ∠CB'O = CA'O.
∠CB'A' = 90° - ∠OB'A' и ∠CA'B' = 90° - ∠OA'B'.
Тогда ∠CA'B' = ∠CB'A' ⇒ ΔCB'A' - равнобедренный и CB' = CA'.
(можно сразу сказать, что CB' = CA' - как отрезки касательных, проведённые из одной точки).
Теперь осталось доказать, что CB' = p (или CA' = p), где p - полупериметр.
B'A = AC', C'B = BA' - как отрезки касательных, проведённые из одной точки.
Тогда AC = CB' - AC'
CB = A'C - BC'